Ondes et signaux
I - Ondes mécaniques
1) Les ondes
a. Rappels
Voir le cours de seconde correspondant en cliquant ici.b. Détermination de la vitesse du son dans l'air
- L'énoncé au format odt (modifiable) au format pdf (non modifiable)
- L'expérience
- Le tableur pour les mesures
- Le fichier arduino
c. Le cours
II - Images et couleurs
1) Formation d'une image à l'aide d'un dispositif optique
a. Présentation
Lorsque l'on regarde à travers une lentille, on voit une image agrandie ou rétrécie, à l'endroit ou à l'envers de l'objet que l'on observe.
.
Cette particularité s'explique par le phénomène de réfraction vu en 2nde(cliquer ici pour vous le remémorer).
Il existe deux types de lentilles, les lentilles convergentes et les lentilles divergentes que l'on vous a déjà présentées en 4ème(cliquer ici pour vous le remémorer).
Nous n'allons nous intéresser qu'aux lentilles convergentes dans la suite de ce chapitre.
TP : Formation d'une image à l'aide d'une lentille
b. Schématiser une lentille convergente
Voici la norme de représentation d'une lentille convergente (un segment terminé par une flèche à chaque extrêmité).
On représente également l'axe orthogonal à la lentille et passant par son centre, l'axe optique Δ (la lettre grecque delta majuscule).
On ajoute enfin trois points importants : le centre optique O, le foyer objet F placé du côté de l'objet AB et le foyer image F' placé de l'autre côté de la lentille par rapport à l'objet AB.
La distance entre O et F' est caractéristique de chaque lentille : c'est la distance focale notée f' qui s'exprime en mètres (m).
En optique on utilise plutôt la vergence V qui s'exprime en dioptries δ (la lettre grecque delta minuscule).
Lorsque l'on regarde à travers une lentille, on voit une image agrandie ou rétrécie, à l'endroit ou à l'envers de l'objet que l'on observe.
.
Cette particularité s'explique par le phénomène de réfraction vu en 2nde(cliquer ici pour vous le remémorer).
Il existe deux types de lentilles, les lentilles convergentes et les lentilles divergentes que l'on vous a déjà présentées en 4ème(cliquer ici pour vous le remémorer).
Nous n'allons nous intéresser qu'aux lentilles convergentes dans la suite de ce chapitre.
Voici la norme de représentation d'une lentille convergente (un segment terminé par une flèche à chaque extrêmité).
On représente également l'axe orthogonal à la lentille et passant par son centre, l'axe optique Δ (la lettre grecque delta majuscule).
On ajoute enfin trois points importants : le centre optique O, le foyer objet F placé du côté de l'objet AB et le foyer image F' placé de l'autre côté de la lentille par rapport à l'objet AB.
La distance entre O et F' est caractéristique de chaque lentille : c'est la distance focale notée f' qui s'exprime en mètres (m).
En optique on utilise plutôt la vergence V qui s'exprime en dioptries δ (la lettre grecque delta minuscule).
L'orientation de l'axe optique est déterminé par la direction des rayons lumineux (qui partent de l'objet vers la lentille) : si l'objet se trouve à gauche de la lentille, l'axe est orienté vers la droite et inversement si l'objet se trouve à droite de la lentille.
Pour davantage de commodité, on représente généralement l'objet à gauche de la lentille, mais ce n'est pas obligatoire !
L'image est ce que l'on peut voir de l'objet lorsque l'on regarde à travers la lentille.
Si on peut former cette image sur un écran ou une feuille de papier, on parle d'image réelle et d'image virtuelle dans le cas contraire.
c. Construire graphiquement l'image d'un objet par une lentille convergente
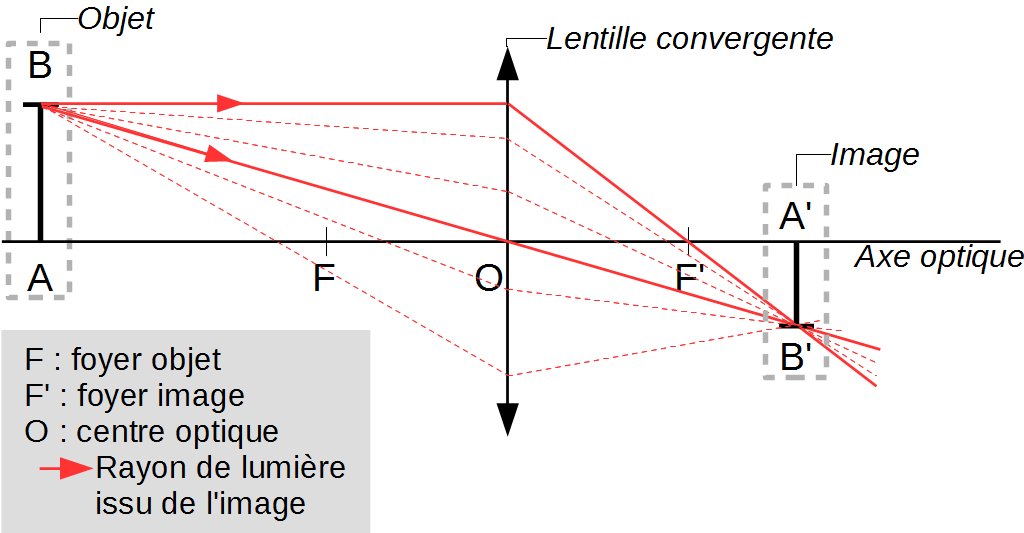
Il suffit pour déterminer sa position de tracer 2 rayon de lumière particuliers issus du sommet B :
- le rayon passant par le centre optique O, qui n'est pas dévié par la lentille,
- le rayon parallèle à l'axe optique Δ qui après avoir traversé la lentille coupe l'axe optique au niveau du foyer image F'.
L'intersection des 2 rayons correspond à l'endroit où se forme l'image B' du point B.
Le point A', image de A est le projeté orthogonal de B' sur Δ.
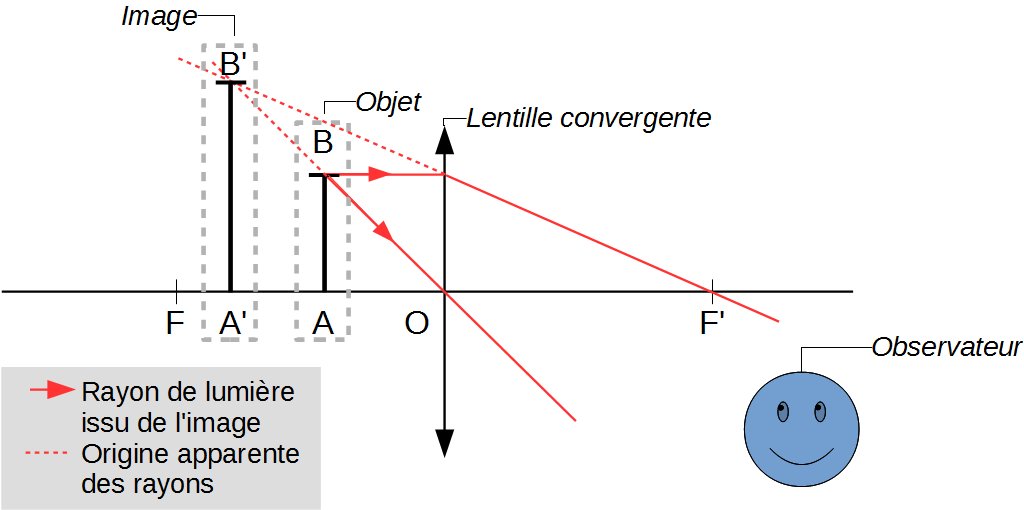
Cela signifie que la lumière semble provenir de l'image virtuelle qui paraît se trouver avant l'objet.
On trace donc de nouveau les deux rayons de lumière définis précédemment, à la différence que l'on va prolonger le rayon passant par le centre optique et le rayon passant par le foyer image de façon à ce qu'ils puissent se couper en amont de l'objet.
Ci-dessous, vous pouvez essayer cette animation geogebra.
Il vous est possible de déplacer le point B, Le foyer image F' (comme s'il vous était possible de modifier la vergence de votre lentille) pour voir comment l'image se forme, réelle ou virtuelle (avec les traits en pointillés).
Challenge : aller sur le site de geogebra, installer le logiciel sur votre machine si ce n'est pas déjà fait (sinon le téléchargement est ici) et essayer de reproduire mon animation.
Si vous y parvenez, c'est probablement que vous avez compris l'essentiel !
d. Relations de grandissement et de conjugaison
L'axe optique est l'axe des abscisses, orienté dans la direction des rayons lumineux, l'origine est le centre optique de la lentille.
Les points A,B,A',B' ont donc pour coordonnées respectives [xA,yA], [xB,yB], [xA',yA'], [xB',yB'].
Il est possible de trouver par le calcul la position de l'image A'B' de l'objet AB en utilisant la relation de conjugaison.
Attention : ne pas oublier le signe des coordonnées !
Le grandissement γ d'une lentille est le rapport entre la taille de l'image et la taille de l'objet.
Si γ est positif, l'image est dans le même sens que l'objet sinon elle est inversée.
Si |γ|>1, l'image est agrandie.
Utiliser la relation de conjugaison
On place un objet AB à une distance OA= ___cm d'une lentille convergente de distance focale OF'= ___cm.L'image A'B' se forme à une distance OA'=cm.
Cette image est réelle ou virtuelle.
Si AB= ___cm, alors A'B'=cm.
2) Couleur des objets
a. Qu'est-ce que la lumière visible ?
Vous avez vu en classe de seconde que la lumière était une onde électromagnétique et ses caractéristiques (cliquer ici pour vous le remémorer).
Le spectre des ondes électromagnétique est très large et la lumière visible ne correspond qu'à la fraction de ce spectre que nos yeux sont capables de voir.
b. Qu'est ce que l'on appelle couleur ?
Il semble nécessaire de comprendre cette notion pour pouvoir traiter la suite du cours.
La "couleur" d'un objet est une sensation que transmet l'oeil au cerveau et que celui-ci interprète.
Elle dépend de certaines caractéristiques de l'objet, mais n'a aucun sens sans observateur doté d'un oeil humain.
La couleur spectrale est la lumière monochromanique donnant la même sensation de couleur qu'un objet coloré de référence. Cependant certaines couleurs n'ont pas d'équivalent spectral comme le magenta
Cela semble aller de soit, mais un animal doté d'un oeil légèrement différent du notre (un oiseau par exemple) et à qui on aurait appris à reconnaître des couleurs monochromatiques ne serait pas forcément d'accord avec son expérimentateur sur la couleur qu'affiche un téléviseur (sa lumière n'est pas monochromatique).
Ce sujet est développé dans un article du magasine Pour la Science. (lien vers l'article (payant))
c. Comment l'œil perçoit-il les couleurs ?
Une histoire de cônes et de bâtonnets
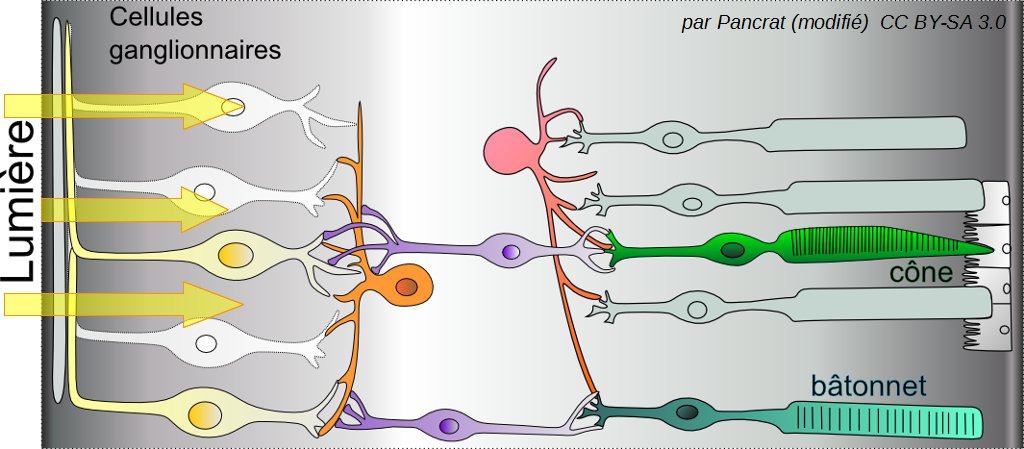
Il y a deux types de cellules chargées de capter la lumière à l'intérieur de nos yeux : les bâtonnets et les cônes.
- Les bâtonnets se chargent de percevoir principalement les faibles lumières, en noir et blanc.
- Les cônes sont responsables de la vision des couleurs. Chez l'Homme, il existe trois types de cônes sensibles à trois domaines de couleurs : celles proches du bleu, celles proches du vert et celles proches du rouge.
Ainsi on dit que l'homme est trichromate puisqu'il a 3 types de cônes. La plupart des mammifères sont dichromates, certains oiseaux sont tétrachromates (4 types de cônes).
"La nuit, tous les chats sont gris"
Pourquoi disposer de bâtonnets qui ne nous permettent que de voir en noir et blanc ? C'est qu'ils sont beaucoup plus sensibles aux faibles lumières que les cônes !
Ainsi la nuit, la lumière est trop faible pour permettre aux cônes de fonctionner : nous voyons en noir et blanc. De plus les bâtonnets sont davantage présents en bordure de l'œil qu'en plein milieu : une faible lumière que l'on perçoit du coin de l'œil dans l'obscurité disparaîtra si l'on cherche à la regarder de face.
Comment notre cerveau interprète une couleur ?
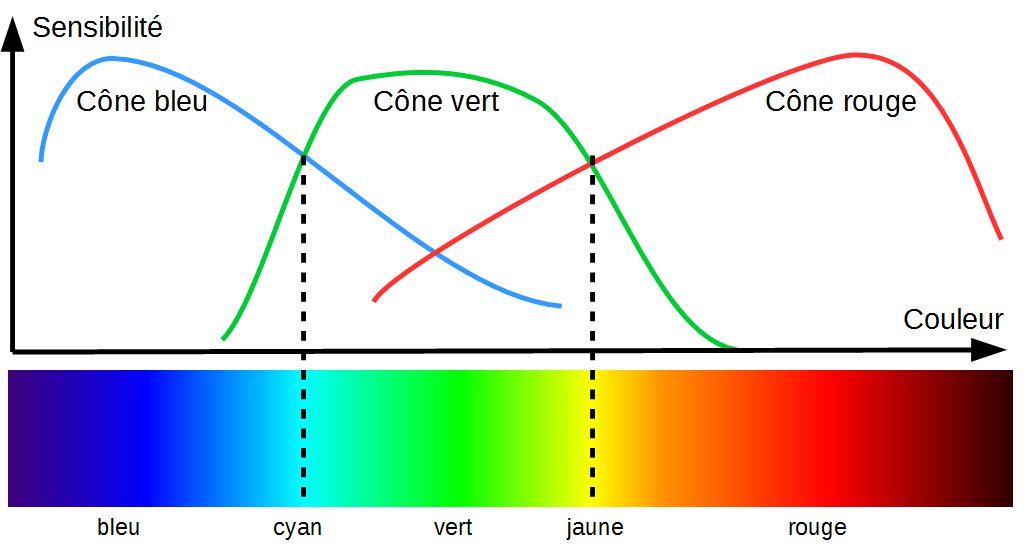
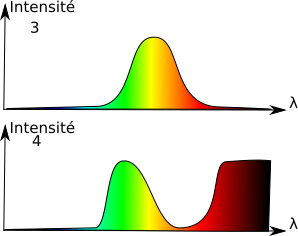
Le cerveau fait la relation : "Si je reçois autant de signal de la part des cônes verts que des cônes rouges, c'est que je suis en train de regarder du jaune !"
Ainsi de suite pour les autres couleurs : le cerveau les interprète en comparant entre eux les signaux émis par les différents cônes.
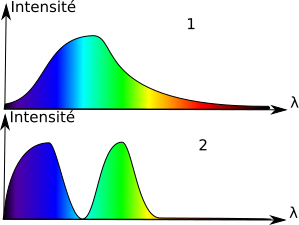
Ci-dessus, l'exemple de deux spectres (1 et 2) qui aboutiront à une sensation de cyan et deux autres (3 et 4) qui aboutissent à la sensation de jaune. On notera pourtant que le 2 ne contient pas de cyan et que le 4 ne contient que peu de jaune !
Enfin, si les trois types de cônes sont stimulés avec des intensités comparables, ou bien s'il fait nuit et que seuls les bâtonnets fonctionnent, leur cerveau interprètera cela comme une lumière blanche.
d. La synthèse additive des couleurs
Lors d'un concert, il est habituel de suivre l'artiste en l'éclairant de différentes couleurs pour changer l'ambiance.
L'accessoiriste ne va pas gérer une centaine de spots en coulisses !
A l'aide de la simulation ci-dessous, essayez d'obtenir les couleurs suivantes : rouge, orange, jaune, vert, bleu cyan, bleu, violet, magenta et blanc. Si, si, c'est possible avec seulement trois manettes !
Il est donc possible de reproduire toutes les couleurs visibles en mélangeant seulement une lumière rouge, une lumière verte et une lumière bleue dans diverses proportions. Ces trois couleurs sont appelées couleurs primaires.
Pour résumer ces mélanges, on a l'habitude d'utiliser la figure de la synthèse additive de la lumière blanche, ci-contre.
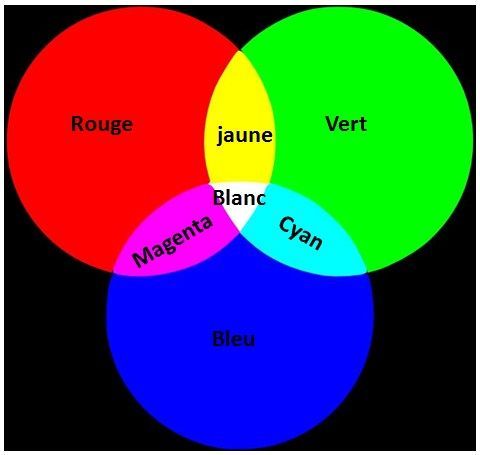
Synthèse additive de la lumière blanche
Comment fonctionnent les TV couleur ?
Puisque nos yeux ne distinguent que 3 couleurs, inutile d'en fabriquer une infinité sur les télévisions : en n'utilisant que 3 lumières proches de la sensibilité maximale des 3 types de cônes, on peut "berner" nos yeux.
Exemple : pour fabriquer du jaune, le téléviseur enverra autant de vert que de rouge. Notre cerveau, en recevant la même intensité de la part des cônes verts et des cônes rouges pensera être en train de regarder du jaune. Cela permet d'expliquer la roue des couleurs primaires…
Comme la lumière blanche est composée de toutes les couleurs, les 3 types de cônes émettent avec la même intensité, ce qui est aussi le cas lorsqu'on leur transmet les trois couleurs primaires rouges, vert, bleu, d'où la sensation de blanc lorsque ces trois couleurs se mélangent.
e. Synthèse soustractive
Introduction
Si la synthèse additive peut être interprétée comme un ajout de couleurs à un spectre n'en contenant initialement aucune, alors la synthèse soustractive est la suppression de certaines couleurs d'un spectre de lumière colorée initial.
C'est ce qu'il se passe lorsque l'ont mélange 2 peintures de couleur différente, que l'on éclaire un objet coloré, ou que l'on intercale un filtre de couleur entre une source de lumière et l'écran sur laquelle elle se projette.
Il est possible de prévoir et d'interpréter les couleurs que l'on obtiendra en fonction des caractéristiques de la source de lumière et de l'objet, de la peinture ou du filtre.
Pourquoi un objet vert est-il vert ?

Pour que l'on puisse voir un objet, il faut qu'il puisse diffuser de la lumière vers notre oeil.
Si un objet semble vert, c'est qu'il diffuse de la lumière verte et qu'il absorbe les autres couleurs.
Cependant, si la lumière qui l'éclaire ne contient pas la ou les couleurs qu'il diffuse, il semblera noir.
Exemple : La photo ci-contre est initialement éclairée en lumière blanche. Faites passer le curseur de la souris sur les cases situées à côté pour voir comment apparaissent les lumières avec différentes couleurs.
On remarque qu'en lumière rouge, le "1" rouge sur la pile ne se différencie plus du blanc qui l'entoure : le contour diffuse normalement toutes les couleurs, mais puisqu'il n'est éclairé qu'avec du rouge, il ne peut diffuser que du rouge, tout comme le "1" qui devient presque invisible.
f. Source de lumière, objet coloré et couleur apparente
Comme vu précédemment, la couleur apparente d'un objet dépend de la couleur qui l'éclaire et de la façon dont il diffuse la lumière.
Dans l'application suivante, il vous est possible de définir la lumière qui éclairera un objet ainsi qui la façon dont il la diffuse. Cela vous permettra d'obtenir un aperçu de la façon dont cet objet nous apparaîtrait.
III - Modèle particulaire et ondulatoire de la lumière
1) Les domaines des ondes électromagnétiques

Ce cloisonnement s'explique principalement par la nature des phénomènes capables de les générer/détecter
2) Le modèle corpusculaire de la matière
a. Les quanta
On pourrait penser que l'énergie lumineuse est un peu comme un filet d'eau qui coule d'un robinet : on peut en prendre n'importe quelle quantité. C'est ce que l'on nomme une grandeur continue.
Pour répondre à certains (gros) problèmes que proposaient les théories physiques, Max Planck en 1900 propose que cette énergie lumineuse est quantifiée : ce n'est plus un filet d'eau qui coule du tuyau, mais des billes.
Il est toujours possible de prendre approximativement n'importe quelle quantité, mais à la bille prés.
Voici une vidéo de la chaîne "e-penser" sur youtube replaçant cette découverte dans son contexte :

h, constante de Planck (h=6,63.10-34 J.s)
ν, fréquence du rayonnement en hertz (Hz).
b. Le modèle
C'est à partir de cette théorie qu'Einstein en 1905 propose que la lumière elle-même (initialement uniquement considérée comme une onde) est quantifiée : c'est le modèle corpusculaire de la lumière.
Comme il est possible de faire le lien entre la fréquence ν (Hz) et la longueur d'onde λ (m) d'un rayonnement monochromatique dans le vide, on obtient la relation :
h, constante de Planck (h=6,63.10-34 J.s)
c, vitesse de la lumière dans le vide (3.108 m.s-1)
λ, longueur de la lumière dans le vide
L'énergie portée par un seul photon étant généralement très faible, on utilise plutôt l'électronvolt (eV) pour l'exprimer.
1 eV = 1,6 × 10-19 J
c. Les niveaux d'énergie de la matière
Dans la prolongation des travaux de Max Planck et Albert Einstein, Niels Bohr propose en 1913 que la matière ne peut adopter que certaines valeurs d'énergie déterminée.
Ainsi un atome aura un état fondamental dans lequel son énergie sera la plus basse et pourra atteindre d'autres niveaux dits états excités dans lesquels son énergie sera plus grande.
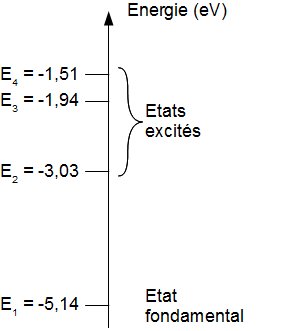
Dans le schéma ci-contre sont représentés les 4 premiers niveaux niveaux d'énergie que peut prendre l'atome de sodium.
Cet atome est capable de se trouver dans n'importe lequel de ces états, mais il n'est pas possible de le trouver dans un état intermédiaire.
d. Niveaux d'énergie et spectre
Dans la prolongation des travaux de Max Planck et Albert Einstein, Niels Bohr propose en 1913 que la matière ne peut adopter que certaines valeurs d'énergie déterminée.
Ainsi un atome aura un état fondamental dans lequel son énergie sera la plus basse et pourra atteindre d'autres niveaux dits états excités dans lesquels son énergie sera plus grande.
Dans le schéma ci-contre sont représentés les 4 premiers niveaux niveaux d'énergie que peut prendre l'atome de sodium.
Cet atome est capable de se trouver dans n'importe lequel de ces états, mais il n'est pas possible de le trouver dans un état intermédiaire.
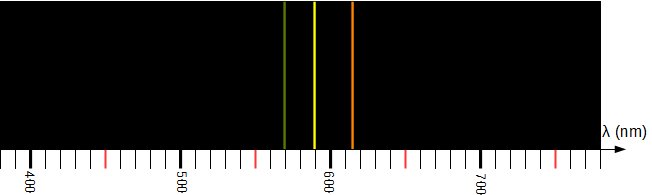
Quand on observe le spectre d'émission d'une lampe à sodium, on observe des raies séparées :
Ce caractère discontinu est correctement prévu par la quantification des niveaux d'énergie.
- Si ΔE = Efinal - Einitial > 0, alors l'atome a absorbé un photon de longueur d'onde - Si ΔE = Efinal - Einitial < 0, alors l'atome a émis un photon de longueur d'onde
Voici les raies spectrales que l'on peut attendre avec les 4 premiers niveaux d'énergie du sodium :
| Energie : | -5.14 | -3.03 | -1.94 | -1.51 |
| -5.14 | ||||
| -3.03 | ||||
| -1.94 | ||||
| -1.51 |
En tant qu'assistant, c'est à vous de l'aider à associer les différentes raies de son spectre d'émission à la transition correspondante entre les différents niveaux d'énergie.