Ondes et signaux

I- Vision et images

1) Réfraction/Réflexion

a. Présentation

Découverte de la loi de Snell-Descartes

Regarder la vidéo présentant diverses expériences autour des phénomènes de réfraction et réflexion
Essayer de reproduire les expériences

	La réfraction : C'est une expérience que vous avez tous fait en allant dans l'eau : lorsque l'on y plonge un objet rectiligne, celui-ci semble brusquement se plier. Sur la photo prise ci-contre, en pointillées sont représentés les contours de la paille si celle-ci n'apparaissait pas courbée.
	La réflexion : En allant à la mer ou à la piscine, vous avez peut-être vu que la surface de l'eau vue de dessous peut ressembler à un miroir. Les deux photos représentent la même scène, mais avec des angles de vue différents. la première, classique, montre le verre et la pièce de monnaie à côté. Dans la seconde, prise en contre-plongée, on aperçoit la pièce qui se reflète sur la surface de l'eau.
	En utilisant la réflexion sur les surfaces du jet d'eau, il est possible de "courber" la trajectoire du rayon laser.

b. Loi de Snell-Descartes

Définitions

A l'aide de l'application ci-dessus, réaliser le TP suivant format LibreOffice ou format PDF et compléter la feuille de calcul.

Cours : la loi de Snell-Descartes

Exemple d'application de la loi de Snell-Descartes.
Un rayon de lumière initialement dans l'air pénètre dans l'eau avec un angle i=30°. L'angle de réfraction du rayon vaut r=22°.

Calculer le rapport $\frac{\sin i}{\sin r}$ .
L'angle d'incidence vaut maintenant i=45, calculer l'angle de réfraction r.
On souhaite maintenant un angle de réfraction r=40°, quel doit être la valeur de l'angle d'incidence i ?
On souhaite maintenant un angle de réfraction r=80°, quel doit être la valeur de l'angle d'incidence i ?

Exercice d'application de la loi de Snell-Descartes.
Un rayon de lumière initialement dans l'air pénètre dans l'eau avec un angle i=__°. L'angle de réfraction du rayon vaut r=__°.

Le rapport $\frac{\sin i}{\sin r}$ a donc pour valeur .
L'angle d'incidence vaut maintenant i=__°, l'angle de réfraction r vaut donc r= °.
On souhaite maintenant un angle de réfraction r=__°, l'angle d'incidence i doit donc valoir i = °.

Remarque : il était indiqué plus haut que la vitesse de la lumière variait dans certains milieux. On peut en fait la calculer grâce à cette valeur !
en effet la vitesse de la lumière dans un milieu transparent vaut :

vitesse de la lumière dans le milieu = \frac{vitesse de la lumière dans le vide}{valeur de \frac{\sin i}{\sin r}}

2) Caractéristiques de la lumière

La lumière se propage en ligne droite
Sa célérité (sa vitesse) dépend du milieu dans lequel elle se propage.
Par convention la célérité de la lumière dans le vide est c₀ = 299 792 458 m.s^-1.
A retenir : célérité de la lumière dans l'air c_air = c₀ = 3,00×10⁸m.s^-1

__ se trouve à une distance d=__km du Soleil.
Un rayon de lumière provenant du Soleil met donc t = secondes à lui parvenir.

Vous pouvez (re)voir l'essentiel de ce qui a été vu sur la lumière ici : cours de 5^ème.

3) Décomposition de la lumière

a. Fabriquer un spectroscope

Un simple dispositif fabriqué à l'aide d'un CD dont on n'a plus l'usage et un tube de rouleau de papier toilette permet de décomposer la lumière provenant d'une source lumineuse.

b. Le spectre de la lumière visible

Si l'on regarde une source de lumière blanche naturelle à l'aide d'un spectroscope, on observe un "arc-en-ciel", dont les couleurs sont toujours dans le même ordre.

Un spectre de lumière blanche

Cela va (de gauche à droite) du violet foncé --> bleu --> cyan --> vert --> jaune --> orange --> rouge

c. Longueur d'onde et couleur monochromatique

On peut considérer que le spectre ci-dessus est constitué d'une infinité de bandes de couleurs diffrentes prises cote à cote. Chaque bande a une couleur unique que l'on peut relier à la longueur d'onde λ (λ est la lettre grecque "lambda").
Cette longueur d'onde λ est généralement exprimée en nanomètre nm :

Un spectre de lumière blanche

Attention : Ce que l'on appelle couleur n'est pas une grandeur mesurable de façon parfaite : c'est une sensation. Elle dépend donc de chaque personne, de son vécu, de sa culture, ...

En revanche la couleur monochromatique correspond à la sensationde référence que donnera un rayonnement monochromatique de longueur d'onde donnée.
Exemple : une longueur d'onde de 480nm correspond à une couleur monochromatique verte et 680nm à une couleur monochromatique rouge.

L'oeil humain est sensible aux ondes électromagnétiques ayant des longueurs d'onde allant de 400nm à 800nm.

Le domaine visible n'est qu'une minuscule partie du spectre électromagnétique !

5) Production de la lumière

Il existe plusieurs façon de produire de la lumière. Le spectrophotomètre va nous permettre d'étudier leurs caractéristiques.
Un spectrophotomètre est capable non seulement de réaliser le spectre d'une source de lumière, mais également de mesurer l'intensité de chaque couleur, cela nous permet de mesurer comment varie l'intensité en fonction de la longueur d'onde.

Les corps chauds

Si l'on réalise le spectrogramme de différentes sources chaudes, on observe des similitudes :

Lampe à filament

Lampe halogène

Soleil

Le spectre d'une source incandescente est continu : toutes les longueurs d'onde sont présentes.
Le spectre présente un maximum d'intensité à la longueur d'onde λ_max.
Plus la température de l'objet est importante et plus λ_max est petit.

Application : cela nous permet d'affirmer que le Soleil a une température supérieure à celle d'une lampe halogène (elle même ayant une température supérieure à celle d'une lampe à filament).

4) Formation d'une image à l'aide d'un dispositif optique

a. Présentation

Lorsque l'on regarde à travers une lentille, on voit une image agrandie ou rétrécie, à l'endroit ou à l'envers de l'objet que l'on observe.
. Cette particularité s'explique par le phénomène de réfraction.
Il existe deux types de lentilles, les lentilles convergentes et les lentilles divergentes que l'on vous a déjà présentées en 4^ème(cliquer ici pour vous le remémorer).

Nous n'allons nous intéresser qu'aux lentilles convergentes dans la suite de ce chapitre.

Formation d'une image par une lentille convergente

Regarder la vidéo présentant diverses expériences autour d'une lentille convergente
Essayer de reproduire les expériences
Réaliser le TP suivant format LibreOffice ou format PDF, avec le fichier Geogebra suivant.

b. Schématiser une lentille convergente

Voici la norme de représentation d'une lentille convergente (un segment terminé par une flèche à chaque extrêmité).
On représente également l'axe orthogonal à la lentille et passant par son centre, l'axe optique Δ (la lettre grecque delta majuscule).
On ajoute enfin trois points importants : le centre optique O, le foyer objet F placé du côté de l'objet AB et le foyer image F' placé de l'autre côté de la lentille par rapport à l'objet AB.

La distance entre O et F' est caractéristique de chaque lentille : c'est la distance focale notée f' qui s'exprime en mètres (m).
En optique on utilise plutôt la vergence V qui s'exprime en dioptries δ (la lettre grecque delta minuscule).

V(δ) = \frac{1}{f'(m)}

L'orientation de l'axe optique est déterminé par la direction des rayons lumineux (qui partent de l'objet vers la lentille) : si l'objet se trouve à gauche de la lentille, l'axe est orienté vers la droite et inversement si l'objet se trouve à droite de la lentille.
Pour davantage de commodité, on représente généralement l'objet à gauche de la lentille, mais ce n'est pas obligatoire !

L'image est ce que l'on peut voir de l'objet lorsque l'on regarde à travers la lentille.
Si on peut former cette image sur un écran ou une feuille de papier, on parle d'image réelle et d'image virtuelle dans le cas contraire.

c. Construire graphiquement l'image d'un objet par une lentille convergente

Formation d'une image réelle par une lentille convergente

Exercice 25 p 298.

Cliquer pour agrandir

Si l'objet est situé avant le foyer image, alors l'image est réelle.
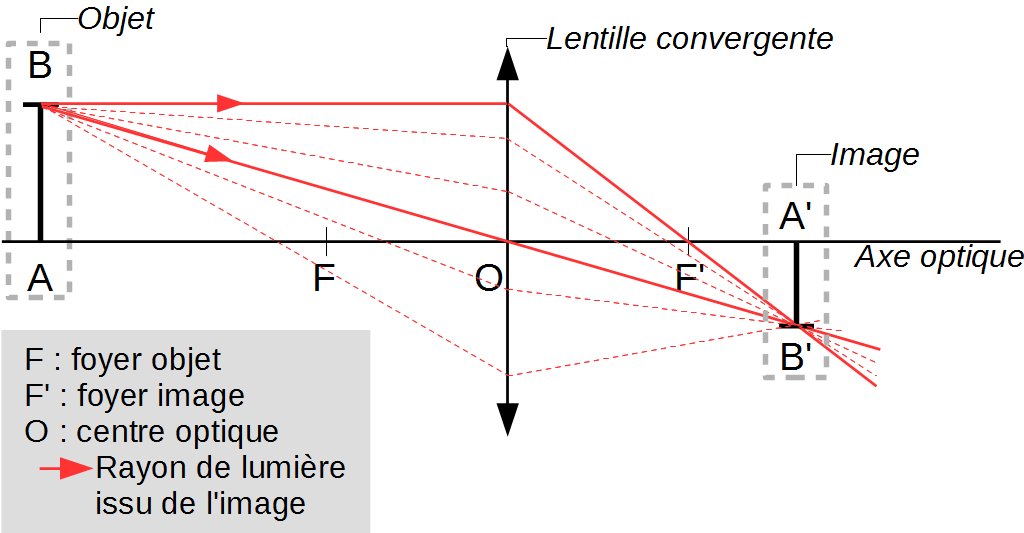
Il suffit pour déterminer sa position de tracer 2 rayon de lumière particuliers issus du sommet B :
- le rayon passant par le centre optique O, qui n'est pas dévié par la lentille,
- le rayon parallèle à l'axe optique Δ qui après avoir traversé la lentille coupe l'axe optique au niveau du foyer image F'.
L'intersection des 2 rayons correspond à l'endroit où se forme l'image B' du point B.
Le point A', image de A est le projeté orthogonal de B' sur Δ.

Cliquer pour agrandir

Si l'objet est situé entre le foyer objet et la lentille, alors l'image est virtuelle.
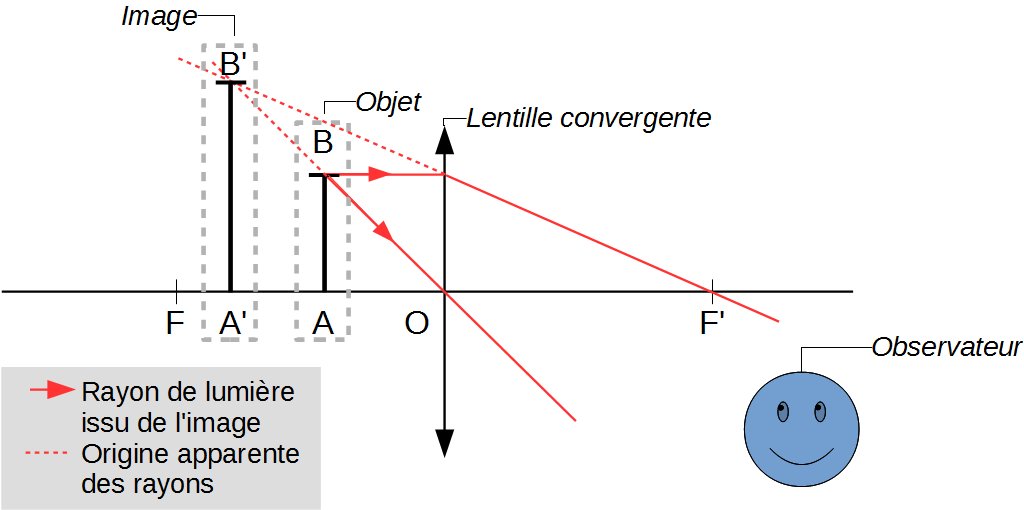
Cela signifie que la lumière semble provenir de l'image virtuelle qui paraît se trouver avant l'objet.
On trace donc de nouveau les deux rayons de lumière définis précédemment, à la différence que l'on va prolonger le rayon passant par le centre optique et le rayon passant par le foyer image de façon à ce qu'ils puissent se couper en amont de l'objet.

Ci-dessous, vous pouvez essayer cette animation geogebra.

Il vous est possible de déplacer le point B, Le foyer image F' (comme s'il vous était possible de modifier la vergence de votre lentille) pour voir comment l'image se forme, réelle ou virtuelle (avec les traits en pointillés).
Challenge : aller sur le site de geogebra, installer le logiciel sur votre machine si ce n'est pas déjà fait (sinon le téléchargement est ici) et essayer de reproduire mon animation.
Si vous y parvenez, c'est probablement que vous avez compris l'essentiel !