Aller au contenu

Algorithmes

I- Recherche par dichotomie⚓

Cliquez sur Fiche dichotomie.pdf pour récupérer l'énoncé du TD.

1) Akinator⚓

Enoncé

Vous jouez Ă  essayer de deviner le nombre auquel pense votre adversaire : en dĂ©but de partie, celui-ci pense Ă  un nombre entre 0 et 100, le note sur une feuille qu’il retourne (pour Ă©viter la triche). Vous devez trouver ce nombre en un minimum de propositions. L’adversaire ne peut dire que "c’est plus", "c’est moins" et "bravo".

  1. Essayez de décrire votre stratégie.
  2. En justifiant votre réponse, indiquez quel serait le nombre minimum de questions à poser afin de trouver le résultat de façon sûre et certaine.
  3. Écrire une fonction akinator(n) qui va chercher Ă  deviner le nombre x auquel vous pensez (0 ≀ x ≀ n) en utilisant la mĂȘme stratĂ©gie que vous.

Corrigé

La meilleure méthode est de diviser systématiquement l'intervalle en deux et de prendre le milieu.
Si par exemple le nombre Ă  trouver est 37, commencer par demander 50 ("c'est moins"), puis 25 ("c'est plus"), puis 37 ("Bravo !").

On se rend compte qu'on a une démarche binaire : comme il est possible de coder 128 nombres sur 7 bits, il est possible de deviner n'importe quel nombre en 7 questions.

Python
def akinator(n):
mini=0
maxi=n
while (maxi-mini)>1 :
    milieu=(maxi+mini)//2
    print("Est-ce qu’il s’agit de :",milieu,"?")
    reponse=input("RĂ©pondre par \"+\" ou \"-\" ou \"oui\"")
    if reponse=="+":
    mini=milieu

    elif reponse=="-":
    maxi=milieu
    else:
    return True

2) Encadrer la solution d'une Ă©quation de type f(x)=0⚓

Enoncé

La fonction f(x)=x3-1,45x2-11,55x+5,39 admet une solution s telle que f(s)=0 avec 0 ≀ s ≀ 1

On donne

Python
def f(x):return x**3-1.45*x**2-11.55*x+5.39
  • Proposer une adaptation de l’algorithme akinator pour trouver une valeur de s arrondie Ă  10-3 prĂšs.
Corrigé
Python
def f(x):return x**3-1.45*x**2-11.55*x+5.39

def resolv(fonction,mini,maxi,intervalle):

while (maxi-mini)>intervalle :
    milieu=(maxi+mini)/2


    if fonction(maxi)*fonction(milieu)>0:
    maxi=milieu

    elif fonction(maxi)*fonction(milieu)<0:
    mini=milieu
    else:
    return milieu

return mini,maxi

La partie la plus compliquée de l'algorithme est mathématique : comment écrire un équivalent de "c'est plus" ou "c'est moins" ?

Il se trouve que si la fonction est strictement monotone et qu'elle admet une solution dans un intervalle, alors les 2 extrĂȘmitĂ©s de cet intervalle n'ont pas le mĂȘme signe => f(mini)×f(maxi)<0.

On teste donc f(maxi)×f(milieu). Si la valeur est positive, c'est que la solution se trouve entre mini et milieu et donc que notre nouvel intervalle est [mini;milieu].

3) Rechercher une valeur dans une liste ordonnĂ©e par dichotomie⚓

Enoncé

Une liste de nombres est générée par la commande

Python
liste=[randint(0,10)]
for i in range(1,100000) :
liste.append(liste[i-1]+randint(1,10))

On souhaite rechercher si un nombre est présent dans cette liste le plus rapidement possible.

  1. D’aprĂšs ce code, la liste est-elle dĂ©jĂ  ordonnĂ©e ? Si oui, en ordre croissant ou dĂ©croissant ?
  2. Est-il possible que la liste contienne deux fois le mĂȘme nombre ?
  3. Écrire une fonction recherche_dicho(nombre,liste) qui recherche par dichotomie le nombre dans liste et retourne si elle le trouve son indice et si elle ne le trouve pas les 2 indices encadrant la position qu’il aurait dĂ» avoir
  4. Utiliser le benchmark de la sĂ©ance algorithmes01 pour vĂ©rifier si cette mĂ©thode est rĂ©ellement plus rapide que l’algorithme indice(liste,valeur) Ă©crit prĂ©cĂ©demment.
    Attention : votre fonction bench gĂ©nĂšre par dĂ©faut une liste alĂ©atoire, ce qui n’est pas le cas de la liste ci-dessus, modifiez la fonction en consĂ©quence !

Corrigé

  1. On voit que chaque terme est égal au terme précédent augmenté de randint(1,10). Cette liste est donc ordonnée en ordre strictement croissant.
  2. répondu juste au-dessus
  3. A vous de chercher !
  4. A vous de chercher !

II- Algorithmes gloutons⚓

Cliquez sur Fiche algo glouton pour récupérer l'énoncé du TD.

1) Introduction⚓

Il y a certains problÚmes problÚmes pour lesquels il existent un trÚs grand nombre de solutions. Parmi ces solutions quelques unes sont optimales, mais l'écrasante majorité ne le sont pas. Il n'est dans certains cas pas possible de trouver une solution optimale car cela demanderait un nombre de calculs hors de portée ou trop coûteux par rapport aux moyens à disposition.

Dans ce cas, il peut ĂȘtre intĂ©ressant de disposer d'un algorithme qui, s'il ne donne pas la solution optimale, est tout du moins capable de trouver une solution, de prĂ©fĂ©rence pas trop mauvaise.

Ce genre d'approche, on l'a déjà abordée au moins une fois : pour faire sortir le robot du labyrinthe : en gardant toujours le mur à droite, on s'assure de pouvoir sortir, mais on ne trouvera généralement pas le trajet le plus court vers la sortie.

Les algorithmes gloutons répondent à cette problématique

En choissant systématiquement l'option qui les rapproche le plus de l'objectif, ils permettent de trouver une solution qui si elle n'est pas systématiquement optimale est généralement satisfaisante.

2) ProblĂšme du rendu de monnaie⚓

Enoncé

Caisse automatique

photo d'une caisse automatique

Vous ĂȘtes employĂ© par l’entreprise CashExpress, spĂ©cialisĂ©e dans la vente de caisses enregistreuses automatiques : pour Ă©viter les contacts entre les employĂ©s et la clientĂšle, le client dĂ©pose directement l’argent dans un automate qui se charge de lui rendre la monnaie.

On suppose que la monnaie peut-ĂȘtre rendue avec toutes les piĂšces et billets existant en euros :

Python
[200, 100, 50, 20, 10, 5, 2, 1, 0.5, 0.2, 0.1, 0.05, 0.01]

(En effet, les billets de 500€ ne sont plus produits depuis 2018)

  1. Un client vous prĂ©sente un billet de 50€ pour payer sa chocolatine a 0,85€, indiquez le dĂ©tail du rendu de monnaie que vous allez faire.
    Un algorithme évident afin de rendre systématiquement correctement la monnaie, serait de rendre uniquement des piÚces de 1 cent.
    Cela présente 2 inconvénients majeurs :
    • il est nĂ©cessaire de prĂ©voir un trĂšs gros volume de piĂšce de 1 cent afin de pouvoir continuer Ă  rendre la monnaie tout au long de la journĂ©e
    • Vous risquez d’irriter vos clients
  2. Proposez une stratégie vous permettant systématiquement de rendre la monnaie en utilisant un nombre minimal de piÚces/billets.
  3. Écrire la fonction rendu_monnaie(montant) qui retourne un dictionnaire contenant le dĂ©tail du rendu de monnaie pour un montant donnĂ©.

Exemple : Le client a payĂ© sa baguette Ă  1,05€ avec un billet de 5€ → l’automate doit lui rendre 3,95€

Text Only
rendu_monnaie(3,95) &rarr;  &#123;'200':0, '100':0, '50':0, '20':0, '10':0, '5':0, '2':1, '1':1, '0.5':1, '0.2':2, '0.1':0, '0.05':1, '0.01':0&#125;
En effet, le rendu optimal est 2€ + 1€ + 50ct + 2x20ct + 5ct

Une boulangerie basĂ©e en Absurdistan souhaite se procurer une de vos machine. Leur monnaie est le Plouk, dont le taux de change est proche de l’Euro : 1 Pk = 1 €.
Leur monnaie est différemment échelonnée : [200, 100, 30, 20, 5, 2, 1, 0.3, 0.1, 0.05, 0.01]

  1. En adaptant la fonction rendu_monnaie(montant) aux différentes valeurs disponibles dans ce pays, quel retour propose-t-elle pour 45 Pk ?
    Ce rendu est-il optimal ?

Corrigé

  1. Je dois lui rendre 50 - 0.85 = 49.15€
    Le meilleur rendu est 2×20€, 1×5€, 2×2€, 1×0.10€, 1×0.05€.
  2. Pour rendre le moins de monnaie possible, il faut toujours rendre la plus grande valeur possible.
  3. c.
Python
monnaie=[200,100,50,20,10,5,2,1,0.5,0.2,0.1,0.05,0.02,0.01]

def rendu_monnaie(montant,monnaie):
    rendu={}
    montant=int(100*montant)
    for piece in monnaie:
        if montant>=100*piece:
            rendu[piece]=int(montant//(piece*100))
            montant-=rendu[piece]*(piece*100)

    return rendu

Il faut faire attention à la façon dont Python travaille sur les nombres flottants.

Pour Ă©viter un problĂšme, il faut s'assurer que les nombres sont entiers en les mutipliant par 100.

  1. Une fois le programme ci-dessus écrit de cette façon, il suffit d'ajouter une nouvelle liste pour les piÚces en Plouks.

Python
monnaie_Pk=[200, 100, 30, 20, 5, 2, 1, 0.3, 0.1, 0.05, 0.01]

On lance ensuite

Python
>>> rendu_monnaie(45,monnaie_Pk)
{30: 1, 5: 3}

L'algorithme propose alors de rendre 4 devises, tandis que la solution optimale Ă©tait de 3 : 2×20Pk, 1×5Pk.

3) Les fractions Ă©gyptiennes⚓

Si les Ă©gyptiens ne connaissaient pas la notation dĂ©cimale, ils connaissaient les fractions, sous une forme particuliĂšre (voir WikipĂ©dia ) : leurs fractions Ă©taient de la forme 1p oĂč p ∈ ℕ * . On parle de fraction unitaire.

Ils pouvaient donc Ă©crire n’importe quel nombre rationnel (un nombre qui peut s’écrire comme le quotient de 2 nombres entiers) en le dĂ©composant d’une infinitĂ© de façons Ă  l’aide de fractions unitaires.

Par exemple 25 = 1 5+ 1 6+ 1 30 = 1 5+ 1 8+ 1 20+ 1 40 .

Cette solution les satisfaisait probablement d’autant plus qu’il n’est pas sĂ»r qu’ils savaient que certains nombres ne pouvaient ĂȘtre rationnels, comme √2 ou π!

Enoncé

Il vous faudrait Ă©crire un algorithme glouton egypte(nombre) qui dĂ©compose n’importe quel nombre 0<x<1 en somme de fractions unitaires


Bien sûr, du fait des spécificités de la prise en charge des nombres et le fait que certains nombre se décomposent nécessairement en une somme infinie de fractions, il faudra accepter une approximation de cette décomposition.

Corrigé
Python
def egypte(nombre,epsilon=1e-7):
    n=2
    sortie=""
    while nombre&gt;epsilon:
        if 1/n&lt;=nombre:
            nombre-=1/n
            sortie+="+1/"+str(n)
        n+=1
    return sortie[1:]</pre>

L'algorithme est "simple" : il part de la fraction 1/2 puis comme dans le problÚme du rendu de monnaie, regarde s'il peut retrancher la fraction à la valeur à décomposer. Le cas échéant, il ajoute son écriture à la décomposition. Il continue jusqu'à ce que le reste soit inférieur à une valeur de référence facultative epsilon.

Python
>>> egypte(2/3)
'1/2+1/7+1/43+1/1807+1/3263443'

Remarque

Cette façon de dĂ©composer un nombre dĂ©cimal devrait vous rappeler quelque chose, puisque c’est de cette façon que l’on dĂ©termine l’écriture binaire d’un dĂ©cimal, en utilisant des fractions unitaires de la forme 1 2n .

4) Le voleur⚓

Il s'agit d'un grand classique de l'algorithme glouton, vous le retrouverez facilement sur Internet

Marcel Lupin est un voleur prĂ©voyant. Avant de perpĂ©trer ses larcins, il prend soin de lister les objets de valeur prĂ©sents chez ses futures malheureuses victimes. Il n’emporte sur les lieux qu’un seul sac de 50kg, il doit ĂȘtre sĂ©lectif !

Il Ă©tablit donc une liste (enfin, nous dirions plutĂŽt dictionnaire, mais Marcel n’est pas informaticien) des objets prĂ©sents, en indiquant tout d’abord leur masse en kg puis leur valeur en Brouzoufs (c’est la monnaie d’Andorrsbourg, riche petite principautĂ© voisine de l’Absurdistan dans laquelle se dĂ©roule notre histoire).

Cette liste est disponible ci-dessous :

Python
{'A': [4, 54], 'B': [2, 9], 'C': [14, 91], 'D': [14, 4], 'E': [8, 18], 'F': [1, 98], 'G': [5, 56], 'H': [15, 85], 'I': [7, 61], 'J': [3, 83], 'K': [2, 75], 'L': [10, 70], 'M': [7, 73], 'N': [14, 71], 'O': [7, 3], 'P': [6, 75], 'Q': [9, 91], 'R': [14, 16], 'S': [9, 48], 'T': [9, 37], 'U': [13, 83], 'V': [3, 30], 'W': [12, 81], 'X': [3, 72], 'Y': [2, 10], 'Z': [3, 24]}

Enoncé

Proposez une fonction a_voler(dictionnaire) qui pour un dictionnaire donnĂ© retourne la liste des items Ă  voler en prioritĂ© afin d’avoir la plus grande valeur dans le sac.
→ Cette fonction calcule Ă©galement la valeur du contenu du sac.

Corrigé
Python
victime={'A': [4, 54], 'B': [2, 9], 'C': [14, 91], 'D': [14, 4], 'E': [8, 18], 'F': [1, 98], 'G': [5, 56], 'H': [15, 85], 'I': [7, 61], 'J': [3, 83], 'K': [2, 75], 'L': [10, 70], 'M': [7, 73], 'N': [14, 71], 'O': [7, 3], 'P': [6, 75], 'Q': [9, 91], 'R': [14, 16], 'S': [9, 48], 'T': [9, 37], 'U': [13, 83], 'V': [3, 30], 'W': [12, 81], 'X': [3, 72], 'Y': [2, 10], 'Z': [3, 24]}

"""
rech_max cherche la plus grande valeur d'un dictionnaire de listes
en permettant de choisir sur quel indice de la liste on fait la comparaison
"""
def rech_max(dictionnaire,indice):
    cles=list(dictionnaire.keys())
    max=dictionnaire[cles[0]][indice]
    cle_max=cles[0]
    for i in cles:
        if dictionnaire[i][indice]&gt;max:
            max=dictionnaire[i][indice]
            cle_max=i
    return cle_max

"""
la fonction a_voler(dictionnaire,capacite_sac) fait 3 choses
- calcule la valeur/kg de chaque objet et l'ajoute au dictionnaire
- ajoute récursivement l'objet le plus rentable dans le dictionnaire 'sac',
    Ă  la condition que celui-ci puisse encore rentrer
- supprime cet objet dans le dictionnaire
"""
def a_voler(dictionnaire,capacite_sac):
    sac={}
    valeur=0
    for i in dictionnaire.keys():
        dictionnaire[i].append(dictionnaire[i][1]/dictionnaire[i][0])
    while capacite_sac&gt;0 and len(dictionnaire)&gt;0:
        cle_max=rech_max(dictionnaire,2)
        if dictionnaire[cle_max][0]&lt;=capacite_sac:
            print("on ajoute",cle_max,dictionnaire[cle_max])
            capacite_sac-=dictionnaire[cle_max][0]
            sac[cle_max]=dictionnaire[cle_max]
            valeur+=dictionnaire[cle_max][1]
        del(dictionnaire[cle_max])
    return valeur,sac

#lancer la fonction avec <strong>a_voler(victime,50)
#la fonction remplira un sac de 50kg avec les objets de victime

La principale difficulté de cet algorithme est de trouver à quel paramÚtre appliquer l'algorithme glouton ! Ce n'est pas forcément la valeur de l'objet, car celui-ci peut valoir beaucoup mais remplir le sac à lui seul.

Le paramÚtre de la valeur rapportée au kilogramme est plus judicieux, car il nous assure de maximiser le butin à chaque prise. En revanche, cet algorithme ne sera pas forcément optimal !

Je vous laisse chercher un exemple dans lequel ce ne sera pas le cas :)

III- Algorithme des k-plus proches voisins⚓

1) Intelligence Artificielle et dĂ©termination⚓

Un problÚme classique pour ce que l'on appelle "Intelligence Artificielle" est celui de la détermination : étant donné un objet, défini par une série de valeurs (taille, poids, valeur, durée, ... ) et (au moins) 2 groupes différents A et B aux caractéristiques différentes, on aimerait déterminer si l'objet appartient au groupe A ou au groupe B.

Les applications sont trĂšs larges :

  • Le visage en photo est-il celui d'un homme ou d'une femme ?
  • Le tableau est-il de Claude Monet ou d'Edouard Manet ?
  • La balance connectĂ©e pĂšse-t-elle un adulte ou un enfant ?

Il existe beaucoup d'algorithmes permettant de réaliser cette tùche, nous allons étudier l'un des plus abordables, celui des k-plus proches voisins.

2) Principe⚓

Pour pouvoir déterminer l'appartenance d'un objet à un groupe, il faut à l'avance connaßtre les paramÚtres de chaque groupe. Seulement les données étant rarement complÚtes (et parfois les concepteurs sachant pas à l'avance quel sera le paramÚtre le plus judicieux), on donne plutÎt un jeu de données contenant les paramÚtres de plusieurs objets auxquels un groupe a déjà été attribué (par un ensemble de spécialistes ou via les réponses aux Captchas que vous validez sur internet).

On compare ensuite pour chaque nouvel objets ses dimensions par rapport aux objets de chaque groupe et on détermine le groupe de cet objet comme étant celui dont il est le plus proche.

Il nous faut donc :

  • Un ensemble d'objets ayant des mesures et appartenant Ă  un groupe dĂ©fini
  • Un objet ayant des mesures et dont le groupe est Ă  dĂ©terminer
  • DĂ©terminer comment on mesure la distance des objets entre eux

Voyons cela au travers de l'exemple le plus courant de cet algorithme :

3) Un problĂšme de fleurs⚓

a. PrĂ©sentation⚓

Saviez-vous qu'il existe plusieurs espĂšces d'iris ?

Iris Setosa Iris Virginica Iris Versicolor

Quand on les regarde, on voit qu'effectivement, elles sont différentes, mais difficile de dire en quoi !

Heureusement, en 1936, Edgar Anderson a mesuré des caractéristiques des différentes espÚces, et notamment :

Fleur Longueur et largeur d'un sépale Longueur et largeur d'un pétale

b. RĂ©cupĂ©ration et visualisation des donnĂ©es⚓

Le fichier iris.txt contient les dimensions des pétales de différentes fleurs ainsi que son espÚce sous la forme

Python
[longueur du pétale, largeur du pétale, groupe]

avec groupe : [0,1,2] → [setosa, versicolor, virginica].

Python
liste_fleurs=[] #On crée une liste vide
with open("iris.txt","r",encoding="utf-8") as txt: 
    for ligne in txt: 
        liste_fleurs.append(eval(ligne[:-1]))

Si l'on trace rapidement un graphique par espÚce avec la longueur du pétale en abscisses et sa largeur en ordonnée pour chaque fleur, on obtient le graphique suivant :

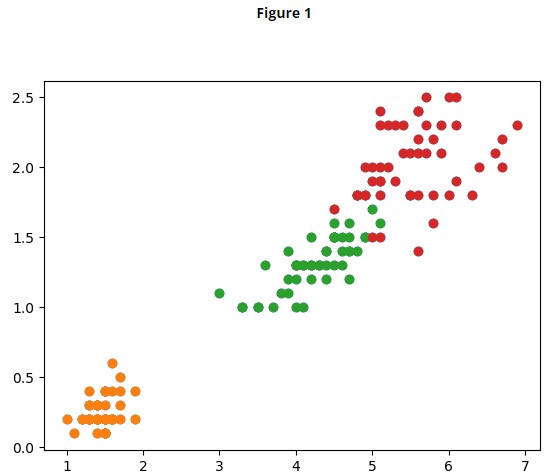
On voit maintenant clairement 3 groupes :

  • en orange, les setosa sont clairement sĂ©parĂ©es des 2 autres espĂšces ;
  • en vert les versicolor ;
  • enfin les virginica, plus grandes, mais dans la continuitĂ© directe des versicolor

Ces groupes, faciles à identifier à l'oeil sont en fait le véritable enjeu de l'algorithme des k plus proches voisins.

c. Calculer les distances⚓

Imaginons maintenant que nous ayons 4 nouvelles fleurs définies par les dimensions de leurs pétales :

  • A : [4,1.2]
  • B : [1.5,0.4]
  • C : [6.5,2.3]
  • D : [5,1.7]

Les fleurs A, B et C sont faciles Ă  placer sur le graphique ci-dessus, mais quid de D ?

Pour dĂ©terminer leur groupe d'appartenance, il va falloir calculer pour chaque fleur A,B,C,D la "distance" Ă  laquelle elle se trouve de chaque fleur du groupe de donnĂ©es. Cette distance peut ĂȘtre dĂ©terminĂ©e de plusieurs façons, considĂ©rons pour ne pas nous compliquer la tĂąche, la distance euclidienne classique

\(AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}\)

Python
def distance(xa,ya,xb,yb):
    return ((xb-xa)**2+(yb-ya)**2)**0.5

def liste_distances(fleur_inconnue,liste):
    distances=[]
    for fleur in liste:
        dist=distance(fleur_inconnue[0],fleur_inconnue[1],fleur[0],fleur[1])
        distances.append([dist,fleur[2]])
    return distances

La commande liste_distances([5,1.7],liste_fleurs) retournera donc une liste récapitulant la distance à laquelle se trouve la fleur D de chacune des fleurs présentes dans le fichier iris.txt.

d. RepĂ©rer les plus proches voisines⚓

Maintenant que l'on connait les distances à chaque fleur, on va devoir déterminer quelle est l'espÚce la plus représentée parmi les plus proches voisines.

Il faut donc :

  • Trier la liste retournĂ©e par liste_distances par ordre croissant
  • Prendre les 5 premiĂšres fleurs et en recenser l'espĂšce

Pour le tri, le plus simple est de reprendre le tri par insertion :

Python
def tri_selection(liste):
    for i in range(len(liste)):
        maxi=liste[0][0]
        indice=0
        for j in range(len(liste)-i):
            if liste[j][0]>maxi:
                maxi=liste[j][0]
                indice=j
        liste[indice],liste[len(liste)-i-1]=liste[len(liste)-i-1],liste[indice]
    return liste

Parmi les k premiers éléments de cette liste on va recenser le nombre de fleurs de chaque espÚce :

Python
def plus_proches(liste,k=5):
    especes=dict()
    for i in liste[:5]:
        if i[1] in especes.keys():
            especes[i[1]]+=1
        else :
            especes[i[1]]=1
    return especes

Finalement, il ne reste qu'à trouver l'espÚce qui est la plus représentée

Python
def recherche_cle_max(dictionnaire):
    liste_cles=list(dictionnaire.keys())
    cle_max=liste_cles[0]
    maxi=dictionnaire[cle_max]
    for i in liste_cles[1:]:
        if dictionnaire[i]>maxi:
            maxi=dictionnaire[i]
            cle_max=i
    return cle_max

Pour connaĂźtre l'espĂšce Ă  laquelle appartient les fleurs A,B,C et D, il suffit donc de faire :

Python
for i in [[4,1.2],[1.5,0.4],[6.5,2.3],[5,1.7]]:
    print(recherche_cle_max(plus_proches(tri_selection(liste_distances(i,liste_fleurs)))))